Matematiksel beklenti. Matematiksel beklenti ayr?k rastgele de?i?ken X sonlu say?da de?er alarak XBen olas?l?klarla RBen, miktar ?u ?ekilde adland?r?l?r:

Matematiksel beklenti s?rekli rastgele de?i?ken X de?erlerinin ?arp?m?n?n integrali denir X olas?l?k da??l?m yo?unlu?u hakk?nda F(X):

(6B)

Yanl?? integral (6 B) kesinlikle yak?nsak oldu?u varsay?l?r (aksi takdirde matematiksel beklentinin oldu?unu s?ylerler) M(X) mevcut de?il). Matematiksel beklenti karakterize eder ortalama de?er rastgele de?i?ken X. Boyutu rastgele de?i?kenin boyutuyla ?rt???r.

Matematiksel beklentinin ?zellikleri:

Da??l?m. Varyans rastgele de?i?ken X numara denir:

Varyans sa??lma ?zelli?i rastgele de?i?ken de?erleri X ortalama de?erine g?re M(X). Varyans?n boyutu rastgele de?i?kenin boyutunun karesine e?ittir. Ayr?k bir rastgele de?i?ken i?in varyans (8) ve matematiksel beklenti (5) ve s?rekli bir rastgele de?i?ken i?in (6) tan?mlar?na dayanarak, varyans i?in benzer ifadeler elde ederiz:

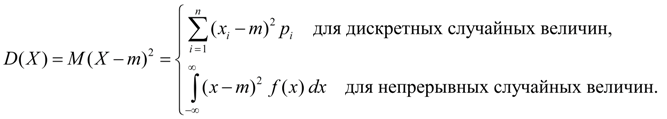(9)

Burada M = M(X).

Dispersiyon ?zellikleri:

Standart sapma:

(11)

Standart sapma rastgele bir de?i?kenle ayn? boyuta sahip oldu?undan, varyanstan ziyade da??l?m ?l??s? olarak kullan?l?r.

Da??t?m anlar?. Matematiksel beklenti ve da??l?m kavramlar?, rastgele de?i?kenlerin say?sal ?zellikleri i?in daha genel bir kavram?n ?zel durumlar?d?r - da??t?m anlar?. Bir rastgele de?i?kenin da??l?m momentleri, bir rastgele de?i?kenin baz? basit fonksiyonlar?n?n matematiksel beklentileri olarak tan?t?lmaktad?r. Yani, sipari? an? k noktaya g?re X 0'a matematiksel beklenti denir M(X–X 0 )k. K?keni hakk?nda anlar X= 0 denir ilk anlar ve belirlenmi?lerdir:

(12)

Birinci dereceden ba?lang?? momenti, s?z konusu rastgele de?i?kenin da??l?m?n?n merkezidir:

(13)

Da??t?m merkezi ile ilgili anlar X= M denir merkezi noktalar ve belirlenmi?lerdir:

(14)

(7)'den birinci dereceden merkezi momentin her zaman s?f?ra e?it oldu?u sonucu ??kar:

Merkezi momentler, sabit bir de?erle kayd?r?ld???ndan beri rastgele de?i?kenin de?erlerinin k?kenine ba?l? de?ildir. ?LE da??t?m merkezi ayn? de?erde de?i?iyor ?LE ve merkezden sapma de?i?mez: X – M = (X – ?LE) – (M – ?LE).
?imdi a??k?a g?r?l?yor ki da??l?m- Bu ikinci dereceden merkezi moment:

Asimetri. ???nc? dereceden merkezi moment:

(17)

de?erlendirmeye hizmet eder da??t?m asimetrileri. Da??l?m noktaya g?re simetrik ise X= M o zaman ???nc? derecenin merkezi momenti s?f?ra e?it olacakt?r (tek s?ralar?n t?m merkezi momentleri gibi). Bu nedenle ???nc? dereceden merkezi moment s?f?rdan farkl?ysa da??l?m simetrik olamaz. Asimetrinin b?y?kl??? boyutsuz bir ?l??m kullan?larak de?erlendirilir. asimetri katsay?s?:

(18)

Asimetri katsay?s?n?n (18) i?areti sa? veya sol taraftaki asimetriyi g?sterir (?ekil 2).

Pirin?. 2. Da??t?m asimetrisi t?rleri.

A??r?. D?rd?nc? dereceden merkezi moment:

(19)

s?zde de?erlendirmeye hizmet eder a??r? normal da??l?m e?risine g?re da??l?m?n merkezine yak?n da??l?m e?risinin diklik (zirve) derecesini belirler. Normal bir da??l?m i?in bas?kl?k olarak al?nan de?er:

(20)

?ek. ?ekil 3'te farkl? bas?kl?k de?erlerine sahip da??l?m e?rilerinin ?rnekleri g?sterilmektedir. Normal da??l?m i?in e= 0. Normalden daha sivri olan e?rilerin pozitif bas?kl??? vard?r, tepesi daha d?z olanlar?n ise negatif bas?kl??? vard?r.

Pirin?. 3. De?i?ken derecelerde dikli?e (bas?kl?k) sahip da??l?m e?rileri.

Y?ksek dereceli momentler genellikle matematiksel istatisti?in m?hendislik uygulamalar?nda kullan?lmaz.

Moda ayr?k Rastgele bir de?i?ken onun en olas? de?eridir. Moda s?rekli rastgele bir de?i?ken, olas?l?k yo?unlu?unun maksimum oldu?u de?erdir (?ekil 2). Da??l?m e?risinin bir maksimumu varsa da??l?m denir. tek modlu. Bir da??l?m e?risinin birden fazla maksimumu varsa bu da??l?ma da??l?m denir. ?ok modlu. Bazen e?rileri maksimumdan ziyade minimuma sahip olan da??l?mlar vard?r. Bu t?r da??l?mlara denir anti-modal. Genel durumda, bir rastgele de?i?kenin modu ve matematiksel beklentisi ?rt??mez. ?zel durumda, modal yani bir modu olan, simetrik bir da??l?ma sahip olan ve matematiksel bir beklentinin olmas? ko?uluyla, da??l?m?n modu ve simetri merkezi ile ?rt??en bir da??l?md?r.

Medyan rastgele de?i?ken X- anlam? bu Meh, e?itli?in ge?erli oldu?u: yani rastgele de?i?kenin e?it derecede muhtemel olmas? X daha az veya daha fazla olacak Meh. Geometrik olarak medyan da??l?m e?risinin alt?ndaki alan?n ikiye b?l?nd??? noktan?n apsisidir (?ekil 2). Simetrik modal da??l?m durumunda medyan, mod ve matematiksel beklenti ayn?d?r.

Mod, bir rastgele de?i?kenin en olas? de?eridir. Ortalamaya g?re simetrik bir da??l?mla mod, matematiksel beklentiyle ?rt???r. Rastgele de?i?kenin de?erleri tekrarlanm?yorsa mod yoktur.

X ekseni ?zerinde da??l?m yo?unluk e?risinin maksimumuna kar??l?k gelen noktaya mod denir, yani mod, rastgele de?i?kenin en olas? de?eridir. Ancak t?m da??t?mlar?n bir modu yoktur. Bir ?rnek, d?zg?n da??l?md?r. Bu durumda da??l?m?n merkezini mod olarak belirlemek m?mk?n de?ildir. Moda'ya genellikle Mo denir.

Rastgele bir de?i?kenin mod ve medyan? kavramlar? vard?r.

A??k?as?, simetrik bir medyan durumunda mod ve matematiksel beklentiyle ?rt??mektedir.

Modun tekil ?l??mlere de?il, geni? hacimli g?zlemlere dayal? olmas? nedeniyle rastgele bir de?i?ken olarak kabul edilemez. Modun b?y?kl???, i?teki ?e?itli gecikmelerden ve normal h?z?n?n kayb?ndan hi?bir ?ekilde etkilenmez.

Bazen ampirik da??l?mlar? analiz ederken, da??l?m?n modu ve medyan? kavramlar? kullan?l?r: "...Mod, bir rastgele de?i?kenin en olas? de?eridir,

Piyango olgusunun kapsaml? bir olas?l?k-teorik yorumu, rastgele bir de?i?kenin olas?l?k da??l?m? kavram?d?r. Onun yard?m?yla, bir rastgele de?i?kenin olas? de?erlerinden birini veya di?erini alaca?? olas?l?klar? belirlenir. Rastgele de?i?keni y ile, olas? de?erlerini ise y ile g?sterelim. Daha sonra Y, y2, VZ, olas? de?erlerini alabilen ayr?k bir rastgele de?i?ken i?in. .., yn olas?l?k da??l?m?n?n uygun bir ?ekli, genellikle olas?l?k serisi, bir da??l?m serisi olarak adland?r?lan P(y = y) ba??ml?l??? olarak d???n?lmelidir. Uygulamada, risk de?erlerinin olas?l?ksal da??l?m?n?n h?zl? genelle?tirilmi? bir de?erlendirmesi i?in, rastgele sonu?lar?n da??l?m?n?n s?zde say?sal ve di?er ?zellikleri s?kl?kla kullan?l?r: matematiksel beklenti, da??l?m, ortalama kare (standart) sapma, varyasyon katsay?s?, mod, medyan vb. (?rne?in bkz. vb.). Ba?ka bir deyi?le, giri?imci h?zl? ve b?t?nsel bir alg? i?in ?abalar (ya da sadece

N?fusun ki?i ba??na ortalama toplam gelire g?re da??l?m?na ili?kin SSCB Devlet ?statistik Komitesi'nden al?nan verilere dayanarak, ortalama, medyan ve modal gelir g?stergelerini kar??la?t?rmaya ?al??aca??z (Tablo 1). Tablo, mutlak de?erdeki ortalama gelirin medyan ve modal geliri a?t???n? ve b?y?mesinin esas olarak y?ksek gelirli insanlar?n pay?ndaki art??tan kaynakland???n?, yani ortalama gelir g?stergesinin kullan?m?n?n ?nemli bir fazla tahmine yol a?t???n? g?stermektedir. N?fusun b?y?k ?o?unlu?unun gelir d?zeyi ve b?y?k ?l??de farkl?la?ma s?recini gizler. Modal gelir de?erleri da??l?m?n alt gruplar?na do?ru y?nelmekte ve medyan gelirden a?a??ya do?ru sapmaktad?r. Bununla birlikte, bir modun bir veya ba?ka bir aral?kta ortaya ??kmas? genellikle rastgeledir; da??l?mdaki k???k bir de?i?iklik, modun biti?ik aral?kta g?r?nmesine neden olur. ?rne?in, 1989'da en yayg?n gelir d?zeyi 100 ila 125 ruble aras?ndayd? (n?fusun %16,1'i bu t?r bir gelir elde ediyordu), ancak 1989-1990'da gelirde meydana gelen k???k de?i?iklikler nedeniyle en yayg?n aral?k ?u ?ekildeydi: aral?k (125-150 ruble) ve modan?n de?eri 15,6 ruble artt?. Ayr?ca, modal gelir aral???nda n?fusun pay? di?er paylar? ?ok az a?abilir.

Logaritmik olarak normal bir rastgele de?i?ken a'n?n da??l?m merkezini karakterize etmek i?in, ?nceden hesaplanm?? matematiksel beklenti Ma ile birlikte, modu (yerel maksimum yo?unluk /(a a)) toc1a = exp(t-st2) ve kullanabilirsiniz.

Mod - moda. Bir rastgele de?i?kenin en olas? de?eri.

MODA - konsept

Moda- bir dizi g?zlemde en s?k meydana gelen de?er

Mo = X Mo + h Mo * (f Mo - f Mo-1) : ((f Mo - f Mo-1) + (f Mo - f Mo+1)),

burada X Mo modal aral???n sol s?n?r?d?r, h Mo modal aral???n uzunlu?udur, f Mo-1 premodal aral???n frekans?d?r, f Mo modal aral???n frekans?d?r, f Mo+1 postmodal aral???n s?kl???.

Mutlak s?rekli bir da??l?m?n modu, da??t?m yo?unlu?unun yerel maksimumunun herhangi bir noktas?d?r. Kesikli da??l?mlar i?in mod, p i olas?l??? kom?u de?erlerin olas?l?klar?ndan daha b?y?k olan herhangi bir a i de?eri olarak kabul edilir.

Medyan s?rekli rastgele de?i?ken X Rastgele de?i?kenin daha az veya daha b?y?k olmas?n?n e?it derecede muhtemel oldu?u de?eri Me olarak ?a?r?l?r Meh yani

M e =(n+1)/2 P(X < ben) = P(X > Meh)

D?zg?n da??t?lm?? NSV

D?zg?n da??t?m. S?rekli bir rastgele de?i?ken, da??t?m yo?unlu?u i?levi varsa, segment () ?zerinde e?it olarak da??t?lm?? olarak adland?r?l?r (?ekil 1.6, A) ?u forma sahiptir:

Tan?m: – SW, ?zerinde e?it olarak da??t?l?r.

Buna g?re segment ?zerindeki da??t?m fonksiyonu (?ekil 1.6, B):

Pirin?. 1.6. Rastgele bir de?i?kenin fonksiyonlar? [ A,B]: A– olas?l?k yo?unluklar? F(X); B– da??t?mlar F(X)

Belirli bir SV'nin matematiksel beklentisi ve da??l?m? a?a??daki ifadelerle belirlenir:

Yo?unluk fonksiyonunun simetrisi nedeniyle medyanla ?ak???r. Modlar?n d?zg?n bir da??l?m? yok

?rnek 4. Bir telefon g?r??mesine cevap i?in bekleme s?resi, 0 ila 2 dakika aral???nda tekd?ze da??l?m yasas?na uyan rastgele bir de?i?kendir. Bu rastgele de?i?kenin integral ve diferansiyel da??l?m fonksiyonlar?n? bulun.

27.Olas?l?k da??l?m?n?n normal yasas?

S?rekli bir rastgele de?i?ken x, parametrelerle normal bir da??l?ma sahiptir: m,s > 0, e?er olas?l?k da??l?m yo?unlu?u ?u ?ekildeyse:

burada: m – matematiksel beklenti, s – standart sapma.

Normal da??l?ma Alman matematik?i Gauss'tan sonra Gaussian da denir. Rastgele bir de?i?kenin m, , parametreleriyle normal da??l?ma sahip olmas? ?u ?ekilde g?sterilir: N (m,s), burada: m=a=M[X];

Form?llerde s?kl?kla matematiksel beklenti ?u ?ekilde g?sterilir: A . Bir rastgele de?i?ken N(0,1) yasas?na g?re da??t?l?yorsa buna normalle?tirilmi? veya standartla?t?r?lm?? normal de?i?ken denir. Bunun i?in da??t?m fonksiyonu ?u ?ekildedir:

Normal e?ri veya Gauss e?risi olarak adland?r?lan normal da??l?m?n yo?unluk grafi?i ?ekil 5.4'te g?sterilmektedir.

Pirin?. 5.4. Normal da??l?m yo?unlu?u

?zellikler normal da??l?m yasas?na sahip rastgele de?i?ken.

1. E?er ise bu de?erin belirli bir aral??a d??me olas?l???n? bulmak i?in ( x 1;) form?l? kullan?l?r:

2. Rastgele bir de?i?kenin matematiksel beklentisinden sapmas?n?n de?eri (mutlak de?er olarak) a?mama olas?l??? ?una e?ittir:

3. "?? Sigma Kural?". Rastgele bir de?i?ken ise, de?erlerinin () aral???nda yer ald??? neredeyse kesindir. (Bu s?n?rlar?n ?tesine ge?me olas?l??? 0,0027'dir.) Kural, parametreleri ( ve ) bilerek, rastgele de?i?kenin pratik de?erlerinin aral???n? yakla??k olarak belirlemeye izin verir.

?stel da??l?m

Bir rastgele de?i?ken X, yo?unlu?unun ?u ?ekilde olmas? durumunda parametreli ?stel bir da??l?ma sahiptir:

Yo?unlu?u entegre ederek ?stel da??l?m fonksiyonunu elde ederiz:

?stel da??l?m?n temel ?zellikleri:

Ortaya ??kan ?stel da??l?m?n yo?unluk grafikleri ve fonksiyonlar?